M2

szabadsugár VIZSGÁLATA

1. A mérés célja

Szabadsugárnak nevezzük az olyan áramlást, amely valamely résen, nyíláson keresztül a nyugvó térbe fúj be. A sugarat környező tér méretéhez képest a sugár térfogata elhanyagolható méretű.

A szabadsugár sajátosságait az ipar számos területén használják (pl. szellőzéstechnika, hűtés, sugárhajtású gépek, stb.).

A mérés célja egy levegő/levegő szabadsugár jellemzőinek vizsgálata.

2. A mérőberendezés leírása

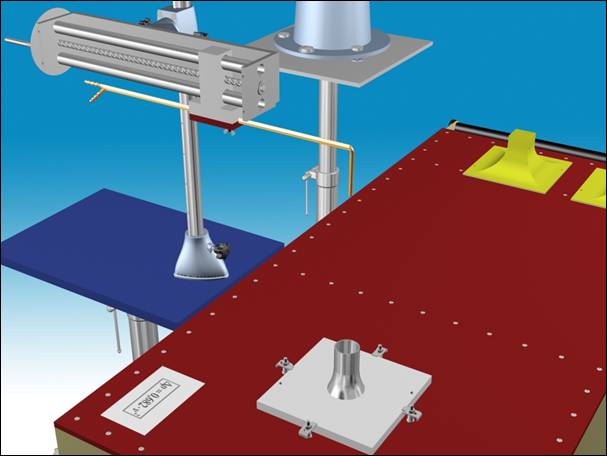
A szabadsugarat a mérőkocsiba szerelt ventilátor állítja elő. A sugár alakját a kifúvás közelében alapvetően a kifúvó elem kilépő keresztmetszete (kör, négyzet, téglalap) határozza meg. A kilépő keresztmetszet egyenletes sebesség-eloszlását a kilépő keresztmetszet megelőző szakaszába épített egyenirányításra szolgáló rácsok, sziták biztosítják. Ezen a szakaszon helyeztünk el két nyomáskivezetést, amellyel a kifúvó átlagsebességhez kapcsolható referencia nyomáskülönbség mérhető. A sebesség változtatását a ventilátor szívóoldali fojtásával érhetjük el.

2.1. Szabadsugár jellemzőinek összefoglalása

A szabadsugár a környezetéből nyugvó levegőrészeket ragad magával, ennek következtében a sugár keresztmetszete, a sebesség-eloszlás, a szabadsugár által szállított térfogatáram változik. A mérés célja ezen jellemzők vizsgálata.

Mérések és elméleti megfontolások alapján a sugár szerkezete a sebességmegoszlás szempontjából két részre osztható (ld. a következő 1. ábra jelöléseit). A ún. magtávolságig a tengelyben – a szabadsugár magjában – a sebesség jó közelítéssel változatlan, a kiáramlási keresztmetszetben érvényes sebességgel megegyezik. A mag mérete pl. hengeres sugárnál a szakirodalom alapján . A szabadsugár rész az ún. lassuló szakasz, ahol , de a sebességmegoszlás, a szabadsugár különböző z távolságban mért sebességprofiljai hasonlók. A sugár szélét a zérus sebességre csökkenő nyíróréteg határolja.

A sugár további jellemzőit az impulzustétel alkalmazásával vizsgálhatjuk, néhány egyszerűsítő elhanyagolással:

a.) a sugár nyugvó térbe áramlik,

b.) a súrlódás és térerő hatását elhanyagoljuk,

c.) a kezdeti kifúvási sebességet időben állandónak tekintjük,

d.) nem vesszük figyelembe, hogy a sugárhoz történő hozzákeveredés folytán (nyírórétegben görbültek az áramvonalak) a sugárban a nyomás kissé eltérő lehet a p₀ környezeti nyomáshoz képest.

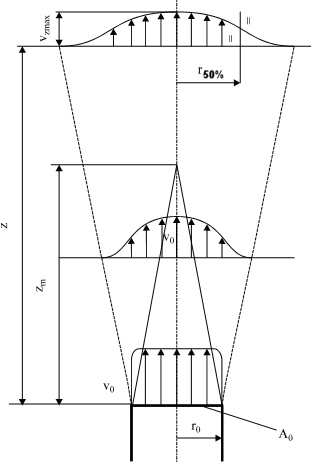
1. ábra Szabadsugár sebesség-eloszlása

A mérési tapasztalatok azt mutatják, hogy ez utóbbi hatás (a görbült áramvonalakból adódó nyomásnövekedés) igen csekély (a kilépő dinamikus nyomás 1%-ánál kisebb). Így ebből a nyomástöbbletből származó erő elhagyható, azaz , ahol A[] a sugarat magába foglaló tetszőleges tér felülete (ellenőrző felület). Az impulzus tételre így közelítést kapjuk. Adott z helyen a sugárra merőleges sugárkeresztmetszetre =áll. érvényes, mivel a sugarat magában foglaló zárt felület a sugár tengelyével párhuzamos alkotókkal határolt felületre a szimmetriát kihasználva: =0.

A sugárra merőleges tetszőleges síkban és természetesen a kilépési keresztmetszetre is igaz, hogy

. (1)

Hozzuk dimenziótlan formába a fenti integrált! A dimenziótlanításhoz használjuk az alábbiakat.

Kör keresztmetszetű hengeres szabadsugár esetén:

Adott sebességprofil maximális sebessége:

A maximális sebesség feléhez (50%-ához)

tartozó sugár a sebességprofil alapján meghatározható:

Ezzel a fenti integrál dimenziótlan alakja:

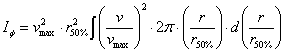(2)

Négyzetes (a×b) kiáramlási keresztmetszet esetén:

Adott sebességprofil maximális sebessége:

A maximális sebesség feléhez (50%-ához)

tartozó x, y távolság a sebességprofilok alapján meghatározhatók: ,

Ezzel a fenti integrál dimenziótlan alakja:

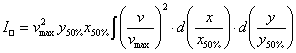(3)

A sebességprofilok a szabadsugár lassuló szakaszán z-től függetlenül hasonlóak, azaz dimenziótlanítva az integrál értéke közel állandó. A lassuló szakasz tengelybeli sebessége, az (1) figyelembevételével kifejezve:

Kör keresztmetszetű hengeres szabadsugár esetén:

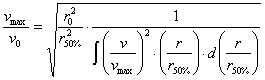(4)

Négyzetes (a×b) kiáramlási keresztmetszet esetén:

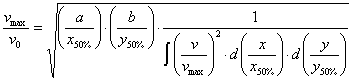(5)

Természetesen a sugár szélesedésére jellemző ill. , értékei a „z” koordináta függvényében méréssel határozhatók meg.

Adott „z” magasságban térfogatáram dimenziótlanított alakja:

Kör keresztmetszetű hengeres szabadsugár esetén:

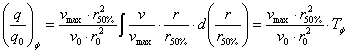(6)

Négyzetes (a×b) kiáramlási keresztmetszet esetén:

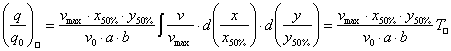(7)

A fenti kifejezés kiszámítása numerikus integrálással hajthatók végre, azaz a mérési pontokban mért értékekkel, mint a folytonos sebességprofilt közelítő értékekből számolt mennyiségekkel határozzuk meg.

3. Mérési feladat; a mérés menete

A szabadsugár sebességprofil méréseket egy kiválasztott kifúvó keresztmetszetnél, és 10 különböző, alább meghatározott „z” magasságban kell elvégezni.

3.1. A kifúvó keresztmetszet kiválasztása és felszerelése a mérőkocsira.

3.2. A vizsgálni kívánt mérési magasságok kiválasztása. A kifúvási keresztmetszet, vagyis a z=0 szint mellett a mérőállványon beállítható legmagasabb mérési magasságot figyelembevéve a kifúvástól számítva a kifúvás d átmérője által meghatározott

z=0, 1d, 2.5d, 5d, 5.5d, 6d, 7d, 8d, 9d, 10d

távolságokban érdemes felvenni a vizsgálni kívánt mérési keresztmetszeteket, amelyekben egy átmérő mentén a sebességprofilt mérjük. Ezek közül minimum 7 keresztmetszetben kell elvégezni a mérést.

3.3. A nyomásmérő műszert annak bekapcsolása után a mérőkocsihoz tartozó gumicsövek segítségével a segédállványon található Prandtl-csőhöz kell csatlakoztatni. Ha Betz-rendszerű manométert használunk, akkor ezt a műveletet járó ventilátornál, a Prandtl-csövet áramlásba helyezve, a csövek óvatos ráközelítésével kell elvégezni, hogy a fordított bekötést a Betz-manométer kitérésének negatív értékek irányába történő elmozdulása révén észlelni lehessen.

3.4. Az adott keresztmetszetben a sebességprofil mérés a v(r) felvételéből áll z=áll. mellett. Ehhez a pozícionáló állványon kell az arra rögzített Prandtl-csövet a kívánt r sugárra mozgatni. A szabadsugár sebességprofil mérését a szabadsugár egyik szélétől a tengelyen át a másik széléig mozgatott Prandtl-csővel kell elvégezni úgy, hogy az adott z magasságban azonos r osztásközt kell alkalmazni. Az alsó tartományban, a kifúváshoz közel 5mm-ként, z mentén távolodva 5-10-15-20 mm-ként kell felvenni a mérési pontokat, tehát a szabadsugár szélesedésével lehet ritkítani a mérési pontokat. Ügyelni kell a pozicionáló állvány beállítására, annak kezdeti nulla (tengelybeli) pozícióját rögzítve, a magasság szerint mozgatva a szabadsugár geometriai tengelyében maradjon!

Az egész állványzat mozgatásakor biztosítani kell, hogy minden mérési szinten tudjuk, hogy hol található a sugár tengelye az eredeti kiáramlási keresztmetszet tengelyéhez képest, ez ugyanis változhat felfelé haladva.

Amint egy mérési pontra beálltunk, meg kell várni, hogy a használt nyomásmérő műszer, a digitális nyomásmérő vagy a Betz-manométer beálljon, viszonylag állandó értéket mutasson (egy kis ingadozás többnyire megmarad, mivel a nagyon pontos műszer az áramlás kis változásait is képes követni). A leolvasott érték a Prandtl-cső működési elvének megfelelően a pontbeli dinamikus nyomás értékét fogja mutatni, melyből az áramlási sebesség számítható.

Minden mérési keresztmetszetben a pozícionáló állványt a geometriai tengelybe (r=0) mozgatva beállítjuk, és a szabadsugár sebességprofilját a sugár szélétől –széléig, vagyis az elsőtől az utolsó mért pozitív sebesség értékig kimérjük. Figyelem! Nem elegendő csak a sugár egyik felét vizsgálni, mivel előfordulhat, hogy a sugár felfelé haladva pl. eltérül, aszimmetrikussá válik!

4. Kiértékelés, a jegyzőkönyv elkészítése

A mérési jegyzőkönyvet a tanszéki honlapon található „jegyzőkönyv követelmények” dokumentum tartalmának figyelembe vételével kell elkészíteni, az alábbi eredmények ismertetésével.

4.1. A leolvasott nyomásértékek megadása táblázatos formában. Célszerű magasságonként egy táblázatot készíteni, mely tartalmazza r függvényében a leolvasott nyomásértéket, annak Pa-ban kifejezett megfelelőjét, az abból számított sebességet, és a térfogatáram számítás későbbiekben ismertetett menetéhez szükséges mennyiségeket.

4.2. Ábrázolandó diagramok: az ábrák valamilyen alkalmas számítógépes szoftver segítségével készítendőek (ügyelve a megfelelő diagram típus kiválasztására – ez az MS-Excel esetében „xy chart”). Ügyeljünk a tengelyek elnevezésére és skálázására, valamint az ábrázolt mennyiségek mértékegységének megadására.

a) A mért sebességprofilok felrajzolása egy közös grafikonban: v(z,r), azaz v=f(z,r).

b) A magtávolságon túl, a lassuló szakaszban mért sebességprofilok egy másik külön, közös diagramban való ábrázolása. v(z,r), azaz v=f(z,r); csak z>z_m profilokra.

c) A magméret meghatározásához a mért profilok maximális sebesség értékeinek ábrázolása a z függvényében: v_max(z), azaz v_max=f(z)

A magméret meghatározása: grafikonban, a z magasság függvényében rögzíteni kell az egyes szinteken leolvasott maximális sebességértékeket. A kapott pontokra görbét illesztve, majd ezt a görbét a v₀ kezdeti legnagyobb sebesség 95 %-ánál meghúzott egyenessel elmetszve és a metszéspontot a magasságot ábrázoló x tengelyre vetítve megkapjuk a z_m magméretet.

d) Dimenziótlan sebességprofilok egy, közös diagramban csak z>z_m profilokra.

v’(z,r’), azaz v’=f(z,r’),

ahol a dimenziótlanított v’ és r’ értékek az alábbiak:

ill.

Tehát a dimenziótlan sebességprofil:

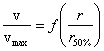
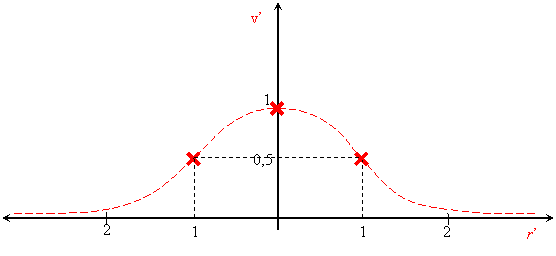
A magtávolságon túli dimenziótlanított sebességprofilok megfelelően elvégzett mérés esetén jó közelítéssel egybeesnek, azon kívül, hogy mindegyiknek át kell haladnia a dimenziótlan grafikon

(r’=0 ; v’=1), és (r’=1 ; v’=0.5)

pontjain. Lásd a következő vázlatot.

e) Minden mérési keresztmetszetre ki kell számítani a szabadsugár által szállított q_V térfogatáramot, majd azt a z függvényében ábrázolni: q_V=f(z). Ezzel szemléltetjük, hogy a szabadsugár a környezetéből levegőt ragad magával. A térfogatáram számításhoz célszerű a következőkben ismertetett egyszerűsítő eljárást alkalmazni.

Az adott mérési magasságon a sugár keresztmetszetét felosztjuk a mérési pontoknak legmegfelelőbb felület elemekre, és minden felület elem keresztmetszetét (DA_i) a hozzá tarozó mért sebességgel szorozva megkapunk egy rész-térfogatáramot (q_Vi). Az adott mérési szint összes mért sebességéhez tartozó ilyen rész-térfogatáramot összegezve kapjuk meg az adott mérési szint teljes térfogatáramát (q_V). A kör keresztmetszetű kifúvó és egy síkban mért sebességértékek esetében a legcélszerűbb a felületet úgy felosztani, hogy minden mért sebességértékhez egy félgyűrű tartozik (kivéve a középen mért értéket, melyhez egy a középső körterület). A félgyűrű vastagsága megegyezik az adott mérési magasságban érvényes mérési pontok közötti lépésközzel (5, 10, 15 vagy 20 mm).

A térfogatáram számításhoz használt A_i felület elemek területét és a kapott q_Vi rész-térfogatáramokat a jegyzőkönyv elején található táblázatban fel kell tüntetni.

A mérési magasságokra számított q_V teljes térfogatáramot a magasság függvényében grafikonban kell ábrázolni, a számított adatpontokat NEM összekötve. A szállított térfogatáram jó közelítéssel lineárisan nő a z távolság függvényében, így a kiáramlási keresztmetszet q₀ térfogatáramából induló lineáris trendvonalat illeszthetünk az adatpontokra. Célszerű egy olyan dimenziótlan térfogatáram diagramot is készíteni, melyben a q₀ térfogatárammal dimenziótlanított értékeket: q’=q_V/q₀ dimenziótlan térfogatáramot ábrázoljuk a z távolság függvényében, mert ekkor azonnal látszik, hogy hányszorosára nő a szabadsugárban szállított levegő térfogatáram a kezdetihez képest

4.6. Hibaszámítás készítése a mérésvezető oktató által meghatározott mennyiségre a tanszéki honlap található hibaszámítási segédlet alapján.

Hibaszámítás

A sebességprofil „k”-ik mérési pontjához tartozó sebesség, abszolút ill. relatív hiba:

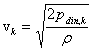
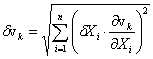
Ahol az X_i mért mennyiségek és a hozzájuk kapcsolódó mérési hibák:

X₁=p₀, dp₀=100 Pa

X₂=T₀, dT₀= 1K

X₃=Dh, dDh= 0.001 m

vagy az EMB-001 nyomásmérő műszert használunk

X₄=p_din, dp_din=2Pa.

Egy sebességprofil minden pontjára ki kell számítani a relatív hiba értékét, és az így kapott hibagörbét kell ábrázolni külön diagramban, amely diagram tartalmazza az adott sebességprofilt is!

A mérés során nem szabad megfeledkezni

-A mérőberendezés bekapcsolása előtt, illetve általában a mérőberendezés üzeme során mindig meg kell győződni a balesetmentes használat feltételeinek teljesüléséről. A bekapcsolásról, illetve a mérés közben végrehajtott változtatásokról a berendezés környezetében dolgozókat figyelmeztetni kell.

- Minden mérési alkalommal a légköri nyomás és teremhőmérséklet feljegyzéséről!

- A felhasznált mérőműszerekről leolvasott értékek mértékegységének és a rájuk vonatkozó egyéb tényezők (Például a ferdecsöves mikromanométer mérőszál ferdítési tényezője.) feljegyezéséről.

- A felhasznált mérőműszerek típusának, gyártási számának és a benne lévő mérőfolyadék sűrűségének feljegyezéséről!

- A mérőműszerről leolvasott mennyiségek és a további számításoknál felhasznált mennyiségek mértékegységének egyeztetéséről.

- Az "U-csöves" nyomásmérő elvén működő mikromanométerek csak megfelelően vízszintezve használhatók.

- Ha nem digitális nyomásmérő kézi-műszert alkalmazunk, akkor a nyomásmérő bekötésénél figyelmesen kell eljárni a csatlakozók "+" illetve "-" ágának és a méréshatár kiválasztásánál. Általában mindegyik manométer típusnál, de kiemelten a ferdecsöves manométernél, figyelni kell arra, hogy a nyomásmérő csatlakozó csonkjaira a gumicsövet óvatosan, "ráközelítve", a mérőfolyadék szál viselkedését figyelemmel kísérve kell felhelyezni. Ha a bekötőcsövek tömör rögzítése előtt a mérőfolyadék szál kitérése megközelíti a maximális kitérést, akkor (ha lehet) méréshatárt kell változtatni a műszeren. Ha ez nem segít, akkor nagyobb nyomások mérésére alkalmas műszert kell választani a méréshez. Ellenkező esetben a mérőfolyadék egy része a bekötőcsőbe áramlik meghamisítva, esetleg teljesen lehetetlenné téve a mérést.

- A nyomásközlő gumi, vagy szilikon csöveket mérés előtt, esetleg közben is célszerű ellenőrizni, nehogy repedés, szakadás legyen rajtuk, mert lyukas mérőcső esetén az összes addigi mérési eredmény kárba vész. Az ellenőrzést szemrevételezéssel, vagy nyomástartási próbával végezhetjük el. Kritikus pontok a műszerekre ill. a nyomáskivezetésekre történő csatlakoztatás helyei.

Irodalom

Lajos Tamás: Az áramlástan alapjai, Műegyetemi Kiadó, Budapest 2004

egyéb segédletek megtalálhatók: www.ara.bme.hu / oktatás / labor oldalon.