M9
diffúzor jellemzőinek
meghatározása
1. A mérés célja:
A laboratóriumi mérés során kör keresztmetszetű diffúzorok
hatásfokát (
) kell meghatározni. A hatásfokot a diffúzor nyílásszöge (j) ill. a térfogatáram (qv) függvényében kell
vizsgálni, majd a mért értékeket diagramban ábrázolni. Három különböző (6°,
15°, 30°) nyílásszögű diffúzor illetve egy Borda-Carnot elem építhető be a mérőberendezésbe.
Az elemek utáni áramlás-egyenletesítő szakasz hossza, valamint a diffúzoron
átáramló levegő térfogatárama is változtatható.
2. A mérőberendezés leírása
Az alábbi 1. ábrán látható a mérőberendezés vázlata. A felső, (7) jelű, ún. kalibráló vezeték segítségével az (5) jelű egyedi kialakítású beszívóelemet egy szabványos átfolyó mérőperemhez (6) kalibráljuk. Az (5) jelű beszívóelem kalibrálása után, azt a mérőszakaszba építve történik a diffúzor hatásfok mérése.
1. ábra: Kalibráló berendezés
2. ábra: Diffúzor hatásfok mérőberendezés
BESZÍVÓELEM KALIBRÁCIÓ
A levegőt a mérőberendezésben egy, az asztalba épített (1) jelű radiális ventilátor áramoltatja, amely szívócsöve a kalibráló-vezetékhez (7) csatlakozik. A kalibráló vezetékbe épített szabványos mérőperemen (6) a (2) sarokmegcsapolásokon mért nyomáskülönbségből meghatározott térfogatáram segítségével meghatározhatjuk a beszívóelemen (5) mért nyomáskülönbség és a térfogatáram kapcsolatát.
DIFFÚZOR HATÁSFOK MÉRÉS
A ventilátor szívócsövét és a beszívóelemet a kalibráló-vezetékről áttesszük a (3) jelű mérőszakaszra. A mérőszakasz és a beszívóelem közé csatlakoztatjuk a vizsgálni kívánt diffúzorokat (4). A térfogatáram az előzetesen kalibrált beszívóelemen mérhető nyomáskülönbség alapján az előzőleg felvett kalibrációs diagram segítségével számítható.
A diffúzor utáni és előtti nyomáskivezetésen ferdecsöves mikromanométerrel vagy digitális manométerrel mért nyomás különbségéből a diffúzor hatásfok számítható. A diffúzor utáni mérőszakaszon több nyomáskivezetés található, hogy figyelembe vehessük a diffúzorban bekövetkező leválás miatt létrejövő, kis nyomásnövekedést eredményező sebesség egyenletesedés hatását.
3. A mérés elve
A következő elvi meggondolásokban mindig a sebességek egész csőkeresztmetszetre vonatkoztatott átlagértékei szerepelnek, és a nyomásokról feltesszük, hogy az egyes keresztmetszetekben állandó. Az „1”–es keresztmetszet a diffúzor belépő, a „2”-es keresztmetszet a kilépő keresztmetszet (illetve a mérőszakasz adott keresztmetszetét) jelöli.
Mit jelent és hogyan határozzuk meg
diffúzor jóságát?
A diffúzort általában akkor alkalmazzuk, ha két különböző keresztmetszetű
szakasz közötti összekötést, azaz adott A1/A2 keresztmetszet-bővítést
kell létrehozni. Ezt célszerű a rendszerbe bevitt legkisebb nyomásveszteség
árán megoldani. A keresztmetszet-bővítést megoldhatnánk egy nagy leválási
veszteségű, hirtelen keresztmetszet-növekedéssel (ún. Borda-Carnot átmenettel),
vagy a másik végletként egy nagy fali súrlódású igen hosszú, bővülő
csőszakasszal is. Az adott áramlást tekintve a legjobb megoldás viszont tulajdonképpen
a két szélsőség közötti legkisebb veszteségtényezőjű, azaz a legjobb hatásfokú,
optimális nyílásszögű diffúzor, lásd alábbi 1. táblázatot.
|
KERESZTMETSZET-NÖVEKEDÉST MEGVALÓSÍTÓ ELEM |
Diffúzor nyílásszög |
RENDSZERBE BEVITT NYOMÁSVESZTESÉG VESZTESÉG OKA |
HATÁSFOK |
|
|
leválás |
fali súrlódás |
|||
|
Borda–Carnot idom (hirtelen
keresztmetszet-növekedés) |
180° |
NAGY |
- |
ROSSZ |
|
Diffúzor |
0°< j
<180° |
KIS |
KIS |
MAXIMÁLIS |
|
Hosszú, bővülő csőtoldat |
Igen kicsi |
- |
NAGY |
ROSSZ |
1. táblázat
Megjegyzés: a tapasztalat azt mutatja, hogy egy 40º nyílásszögnél
nagyobb diffúzor kb. ugyanakkora veszteséget okoz, mintha egy Borda-Carnot
idom.
Egy diffúzor számszerű jellemzésére a diffúzor hatásfokot definiáljuk:
,
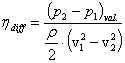amely a tényleges (valós) nyomásnövekedést 
viszonyítja az ideális,
veszteségmentes esetben létrejövő 
nyomásnövekedéshez,
amely az egyszerű Bernoulli-egyenletből számítható:
,
A valós (mért) és az ideális nyomásnövekedés hányadosa a diffúzor hatásfok.
A másik jellemző, amelyet elemek
(könyökök, szelepek, stb.) jellemzésére szoktak használni a 
veszteségtényező, mely
a diffúzor esetében a következő kifejezéssel adható meg:
.
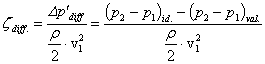A diffúzorban áramló közeg nyomásveszteségét
viszonyítják a belépő dinamikus nyomáshoz. Természetesen a hatásfok és a
veszteségtényező között az alábbi szoros kapcsolat áll fenn (a kifejezés
jobboldali második alakjában a 
alakú kontinuitást is
felhasználva):
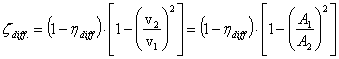
Az
„1” és „2” keresztmetszetek az áramlás irányban vett diffúzor előtti ill. utáni
keresztmetszetek. A diffúzor előtti nyomásmérés helye –mivel a diffúzor
visszahatása jelen esetben elhanyagolható – egyértelmű.
De
melyik nyomáskivezetésnél legyen a “2-es” keresztmetszet? Hol „fejeződik be”,
„meddig tart” áramlástanilag a diffúzor?
Miért
merül fel a fenti kérdés, miért nem rögtön a diffúzor utáni első csonkon mért
adattal számolunk? A zavart a leválás jelensége okozza. Amikor a közeg
keresztmetszet növekedésnek van kitéve, azaz áramlás irányú nyomásnövekedésnek,
várható, hogy leválik a falról és csak bizonyos út megtétele után fekszik
vissza rá. Eközben a közeg sebessége csökken, nyomása nő. Ha ábrázoljuk a mért statikus
nyomáskülönbségeket a diffúzor kilépő keresztmetszetétől mért távolság
függvényében, megfigyelhetjük, hogy a diffúzor hatására létrejövő statikus
nyomás növekedés nem rögtön a diffúzor után éri el a maximumát, hanem csak
fokozatosan. A leválási zóna után is egy darabig növekszik a nyomáskülönbség a diagramunkon.
Azzal az értékkel számolunk, ami már a közel vízszintes szakasz kezdetéhez
tartozik.
Mivel a különböző
diffúzorok különböző térfogatáramoknál más és más méretű leválási zónát
okoznak, a nyomáslefutást mindegyik esetben ábrázolni kell és a „2-es”
keresztmetszet helyét egyenként meghatározni.
4. A mérés lefolytatása
A beszívóelem kalibrálása
A mérés során a szállított qv
[m3/s] térfogatáram
meghatározására a beszívóelem szolgál. A beszívóelemen átáramló közeg
térfogatárama az alábbi összefüggésből számítható:
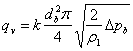
ahol
k [-] beáramlási
tényező
db [m] beszívóelem
belső átmérő (Itt az értéke 36.4 mm)
r1 [kg/m3] áramló közeg sűrűség
Dpb [Pa] beszívóelemen mért nyomásesés
A beszívóelem beáramlási tényezőjét a kalibrálócső segítségével
határozhatjuk meg. A kalibrálócső tartalmaz egy szabványos kialakítású,
sarokmegcsapolásos átfolyó mérőperemet, melynek átfolyási számát szabványban
rögzített ismert módszerrel tudjuk meghatározni. A kalibrálás során különböző
térfogatáramok mérjük a mérőperem és a beszívóelem nyomásesését. A mérőperem
nyomáseséséből meghatározható a szállított térfogatáram, amit összevetve a
beszívóelem nyomásesésével meghatározható annak a beáramlási tényezője. Az beáramlási
tényező meghatározását legalább három térfogatáramon végezzük el, majd
hasonlítsuk össze a kapott értékeket. A berendezésen beállítható viszonylag kis
Re-szám tartomány miatt Re-szám függőséget nem tapasztalunk, ezért a három
esetben kiszámolt átfolyási szám közel azonos értékű lesz. Az átlagértéküket
felhasználva ezek után már alkalmas a beszívóelem térfogatáram mérésre.
Megjegyzés:
A kalibráció folyamata egy általános esetben csupán
annyiból állna, hogy az összetartozó adatokból (pl. itt a mérőperemen
meghatározott térfogatáram – beszívóelem nyomásesése) un. kalibrálási diagramot
szerkesztünk. Ilyenkor a beszívóelem nyomásesése alapján meghatározni kívánt
térfogatáramot minden egyes esetben a diagramról tudnánk leolvasni. Mivel itt azonban lehetőségünk van a
kalibrációt egy paraméter – beszívóelem beáramlási tényező – meghatározására
visszavezetni, a kalibrációs diagramot nem szükséges megszerkesztenünk.
A mérőperemen átfolyó térfogatáram számítási képlete:
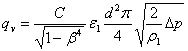
ahol
C [-] átfolyási
tényező
b [-] mérőperem
átmérőviszony (jelen esetben b=0,6587)
e [-] kompresszibilitási
tényező (jelen esetben e=1, mivel a közeg
nyomásváltozása csekély)
d [m] mérőperem furatátmérő (jelen esetben d=38,8mm)
Dp [Pa] mérőperemen
mért nyomásesés
A mérőperemre jellemző C
átfolyási tényező számítási képlete:
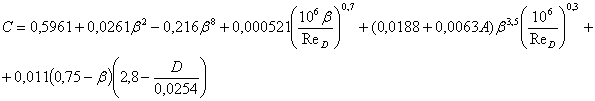
ahol
[-] Reynolds-szám,
a mérőperem előtti csőátmérővel
számolva (jelen esetben D=58,9mm)
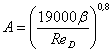
Iteráció
A fent megadott képletek alakján a térfogatáram számítása még nem végezhető
el, hiszen a qv
térfogatáram számításához szükséges C
átfolyási tényező Reynolds-szám függő, így a közeg áramlási sebességétől függ, amelyet
nem ismerünk. (Hiszen ha ismernénk, nem lenne szükség a térfogatáram mérésére.)
A feladat megoldásához így szükségszerű többlépéses iterációt alkalmazni.
Az iteráció lényege, hogy tapasztalat alapján egy közelítő kiindulási értéket
felvéve - pl. a C tényezőre - a
térfogatáram közelítő értéke számítható. Ebből a közelítő térfogatáramból a
csőbeli áramlási sebesség, így a Reynolds-szám valamint a C átfolyási tényező is számítható, és összevethető a kezdetben
felvett C értékével. Ezt az iterációs
számítási ciklust addig ismételjük, amíg két iterációs lépést összehasonlítva a
C értékek közötti eltérés egy %-ban
megadott hibahatáron belül kerül. Jelen esetben pl. 1-2%-os hibahatár
elfogadható pontosságú, a számítás gyorsan konvergál, csak néhány iterációs
lépést igényel, amely pl. Excel-ben könnyen megoldható.
1. lépés
C’ → qV’ → v’ → ReD’ → C’’
2. lépés
C’’ → qV’’ → v’’ → ReD’’ → C’’’
stb.
PÉLDA
Vegyük fel a C átfolyási tényező értékét:
legyen az első iterációs ciklusban C=0,6.
Határozzuk meg a térfogatáram értékét a felvett átfolyási tényezővel. Majd
számoljuk ki az áramlási sebességet a mérőperem előtt, ezzel számoljunk
Reynolds-számot, majd számoljuk ki a képlet segítségével a C átfolyási tényező „új” értékét. Ezt az értéket vessük össze a
felvett 0,6 értékkel: az eltérés a megadott hibahatáron belül van-e? Ez egy
ciklusa az iterációnak.
Amennyiben felvett és kiszámolt érték közötti eltérés nagyobb, mint az 1-2%
hibahatár, a ciklust ismételjük.
A sebesség- és nyomásmérés
A 
és 
sebességeket a
beszívóelem segítségével mért térfogatáramból számoljuk:
, illetve 
A diffúzor belépésénél lévő kivezetés (p1) és az utána levő ún. mérőszakasz
nyomáskivezetései (p2) között kell mérjük a nyomásnövekedést. A mért
nyomásnövekedésből és a sebességekből számítható a diffúzor hatásfoka.
5. A mérés kiértékelése és ellenőrzése irodalmi
adatokkal:
A kiértékelés során a diffúzor geometriai adatait pontosan rögzíteni kell. A mért sebesség és nyomásértékeket táblázatosan és diagramok formájában kell elkészíteni (diagramba: nyomáslefutások ábrázolása: mért nyomások a hely függvényében az összes esetre)
A mérés kiértékelésekor meg kell határozni a diffúzor hatásfokát és veszteségtényezőjét, különböző térfogatáramokon mérve, eredményeket táblázatban és diagramban összefoglalni. (Diagramok szervezése olyan legyen, hogy szemléletesen látszódjon a térfogatáramok hatása, illetve az idomok kialakításának a hatása is. Pl. x tengely: térfogatáram, y tengely: hatásfok, így minden idom egy görbét alkot a diagramban.)
Hibaszámítás:
A diffúzorhatásfok kifejezése, és az abszolút hiba számítása:
A mért értékekkel kifejezve: abszolút
hiba: relatív
hiba:
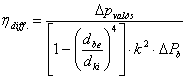
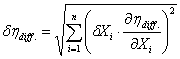
ahol az Xi mért
mennyiségek és a hozzájuk kapcsolódó mérési hibák:
X1,2=d, illetve a csőátmérők mérésének
hibája dd=0.001m
X3,4=Dh, illetve a ferde- v. görbecsöves manométer leolv. hibája dDh=0.001m
Vagy:
X3,4=Dp, illetve a digitális manométer hibája dDp =2 Pa
A hibaszámítás értékét alkalmazni kell a közölt diagramokban és táblázatokban.
(pl. 
)
A mérés során
nem szabad megfeledkezni
-A mérőberendezés
bekapcsolása előtt, illetve általában a mérőberendezés üzeme során mindig meg
kell győződni a balesetmentes használat feltételeinek teljesüléséről. A
bekapcsolásról, illetve a mérés közben végrehajtott változtatásokról a
berendezés környezetében dolgozókat figyelmeztetni kell.
- Minden mérési
alkalommal a légköri nyomás és teremhőmérséklet feljegyzéséről a mérés előtt és
után is!
- A felhasznált
mérőműszerekről leolvasott értékek mértékegységének és a vonatkozó egyéb
tényezők (Például a ferdecsöves mikromanométer mérőszál ferdítési tényezője.)
feljegyezéséről.
- A felhasznált
mérőműszerek típusának, gyártási számának és a benne lévő mérőfolyadék
sűrűségének feljegyezéséről!
- A mérőműszerről
leolvasott mennyiségek és a további számításoknál felhasznált mennyiségek
mértékegységének egyeztetéséről.
- Az
"U-csöves" nyomásmérő elvén működő mikromanométerek csak megfelelően
kivízszintezve használhatók.
- A nyomásmérő
bekötésénél figyelmesen kell eljárni a csatlakozók "+" illetve
"-" ágának és a méréshatár kiválasztásánál. Általában mindegyik
manométer típusnál, de kiemelten a ferdecsöves manométernél, figyelni kell
arra, hogy a nyomásmérő csatlakozó csonkjaira a szilikon csövet óvatosan,
"ráközelítve", a mérőfolyadék szál viselkedését figyelemmel kísérve kell
felhelyezni. Ha bekötőcsövek tömör rögzítése előtt a mérőfolyadék szál kitérése
megközelíti a maximális kitérést, akkor méréshatárt kell változtatni a műszeren.
Ha ez nem lehetséges, akkor nagyobb nyomások mérésére alkalmas műszert kell
választani a méréshez. Ellenkező esetben a mérőfolyadék egy része a bekötőcsőbe
áramlik, meghamisítva esetleg teljesen lehetetlenné téve a mérést
- A nyomásközlő
szilikon csöveket mérés előtt, esetleg közben is célszerű ellenőrizni, nehogy
repedés, szakadás legyen rajtuk, mert lyukas mérőcső esetén az összes addigi
mérési eredmény kárba vész. Az ellenőrzést szemrevételezéssel, vagy
nyomástartási próbával végezhetjük el. Kritikus pontok a műszerekre ill.
a nyomáskivezetésekre történő csatlakoztatás helyei.
Irodalom
Diffúzor
[1]
Nyomásmérés manométerrel
[2]
Térfogatáram mérése beszívó mérőperemmel
[3]