5.
Csoportos feladat: Hátrafelé néző lépcső CFD elemzése k-omega
SST modellel
A feladat áramlás irányában lelépő lépcsővel ellátott
csatornaszakaszban kialakuló áramkép kiszámítása adott tető állásszög (alfa) esetére.
A számítás eredményeit a feladathoz biztosított mérések eredményeivel kell
összehasonlítani.
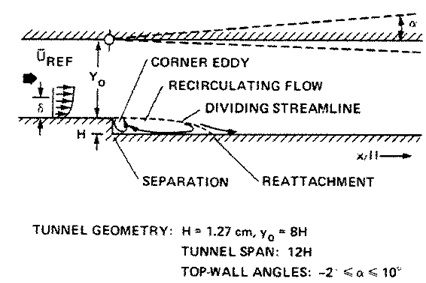
1.ábra Geometriai modell és az áramlás szerkezete
A lépcső egy csatorna oldalában helyezkedik el. A csatorna
állandó szélességű (az ábra síkjára merőleges méret állandó), az áramlás
2-dimenziósnak tekinthető. A csatorna magassága a lépcső előtt Y0(=8H), a lépcső után pedig Y0+H, ahol a lépcső
magassága H. Mivel a tartomány
minden mérete kifejezhető H-val, ezért csak annak értékét mutatjuk az ábrán: H=12.7mm. A lépcső előtt a geometria x=-2H távolságban kezdődik, a lépcső
felső éle az (x=0, y=0) koordinátán kell legyen! A lépcső mögött 15H távolságban kell lennie a kilépés peremfeltételnek! A csatorna
teteje zsanérozott a lépcső síkjával azonos koordinátán (x=0) és különböző
szögekbe dönthető. Ezzel diffúzorossá, illetve konfúzorossá tehető a lépcső utáni csatorna tartomány,
amellyel a nyomás áramlás irányában növelhető, illetve csökkenthető. A tető
beállítási szögét az ábrán α-val (alfa)
jelöltük.
Peremfeltételek
Belépő peremfeltételként egy sebesség és turbulencia profilt
írunk elő, amely a mellékelt bfs_belepes.prof profilfájlban szerepel. Fontos, hogy a
belépő profil a lépcső síkjától visszafelé (az ábrán tőle balra) x=-2H távolságban van, ezért a
geometrián is ott kell lennie. A profil fájl tartalmazza a belépő sebesség
eloszlást, a turbulens kinetikai energia (k), a disszipáció (epszilon), illetve
a specifikus disszipáció (omega) értékeit (utóbbiak a
FLUENT manual javaslatai szerint kiszámolva). A
kilépésnél állandó nyomás peremfeltétel, a falaknál pedig a tapadás törvénye
alkalmazható.
A referencia sebesség, amit az eredmények dimenziótlanítására
kell használni (NEM PEREMFELTÉTEL!!!) Uref=44.2m/s.
1.
Részfeladat (3 pont)
A
geometriai modell elkészítése alfa=-2°, 0°, 6° és 10° esetekre;
Struktúrált hálók elkészítése;
Vegye
figyelembe az alábbiakat:
-
a falak közelében határréteg található, amelynek falra merőleges irányú
felbontására ügyelni kell;
-
a lépcső élén a határréteg leválik és nyíróréteg alakul ki, ezért a nyíróréteg
várható helyén is ügyeljünk a háló megfelelő sűrűségére.
2.
Részfeladat (3 pont)
Megfelelő
peremfeltételek kiválasztása és paramétereik megadása FLUENT-ben;
A
belépő peremfeltételt profil fájl segítségével adja meg!
3.
Részfeladat (3 pont)
Ellenőrizze
a háló megfelelőségét a turbulencia modellek, illetve a kialakult nagy
nyírással jellemzett tartományok megfelelő felbontása tekintetében alfa=0
esetre:
-
ellenőrizze a fali y-plus értékét,
hogy a turbulencia modell által megkövetelt tartományban van-e. Ha nincs,
módosítsa a háló ezen részét;
-
végezzen adaptív sűrítést a szabad nyírórétegek tartományán és
ellenőrizze, hogy mennyit változnak az áramlási jellemzők!
4.
Részfeladat (3 pont)
Végezze
el a számítást k-omega SST turbulencia modell
alkalmazásával négyféle alfa szögre!
- Rajzoltassa ki a sebességeloszlást
a lépcső mögött 1H, 2H, 3H, 4H és 5H távolságban!
- Vesse össze az ön által kapott
visszafekvési távolságot a mérésnél kapott értékkel (xR/H)!
- Vesse össze a nyomástényező (cp) megoszlásokat az alábbi táblázatokban
található mérési adatokkal, ügyelve a referencia értékek helyes beállítására!
Mérési
adatok:
A
visszafekvési pont helye
|
Tető
szöge |
Visszafekvési
hossz |
Hibája |
|
a [°] |
Xr/H |
dXr/H |
|
-2 |
5.82 |
-0.08 |
|
0 |
6.26 |
-0.1 |
|
6 |
8.3 |
-0.15 |
|
10 |
10.18 |
-0.5 |
Nyomástényező
(a) a lépcső oldalán
|
X/H |
a=-2 |
a=0 |
a=6 |
a=10 |
|
-8.5 |
0 |
0.0039 |
0.0117 |
0.0088 |
|
-6.5 |
0 |
0 |
0.0136 |
0.0108 |
|
-4.5 |
-0.0059 |
-0.0048 |
0.0166 |
0.0187 |
|
-2.5 |
-0.0296 |
-0.0231 |
0.0214 |
0.0266 |
|
-0.5 |
-0.0642 |
-0.0472 |
0.0283 |
0.0512 |
|
0 |
-0.0859 |
-0.0607 |
0.0361 |
0.061 |
|
0.5 |
-0.0899 |
-0.0636 |
0.0331 |
0.06 |
|
1 |
-0.0899 |
-0.0665 |
0.0312 |
0.0571 |
|
1.5 |
|
|
0.0292 |
0.0571 |
|
2 |
-0.1017 |
-0.0742 |
0.0253 |
0.0571 |
|
2.5 |
|
|
|
0.0502 |
|
3 |
-0.1037 |
-0.0762 |
0.0185 |
0.0482 |
|
3.5 |
-0.083 |
-0.0665 |
0.0253 |
|
|
4 |
-0.0464 |
-0.0424 |
0.04 |
0.0581 |
|
4.5 |
0.0049 |
0.0077 |
0.0585 |
|
|
5 |
0.0494 |
0.0482 |
0.0829 |
0.0876 |
|
5.5 |
0.0771 |
0.0782 |
|
|
|
6 |
0.1037 |
0.1129 |
0.1297 |
0.1251 |
|
6.5 |
0.1205 |
0.1303 |
|
|
|
7 |
0.1275 |
0.1389 |
0.1667 |
0.1556 |
|
8 |
0.1304 |
0.1515 |
0.1989 |
0.1871 |
|
8.5 |
|
|
0.2115 |
|
|
9 |
0.1225 |
0.1535 |
0.2203 |
0.2117 |
|
9.5 |
|
|
0.231 |
|
|
11 |
0.0978 |
0.1477 |
0.2544 |
0.2551 |
|
12 |
|
|
0.2641 |
|
|
13 |
0.0751 |
0.1409 |
0.2749 |
0.2846 |
|
15 |
0.0534 |
0.1342 |
0.2924 |
0.3073 |
|
17 |
0.0385 |
0.1303 |
0.308 |
0.328 |
|
19.5 |
0.0168 |
0.1285 |
0.3265 |
0.3448 |
|
21.5 |
0.001 |
0.1246 |
0.3402 |
0.3596 |
|
23.5 |
-0.0168 |
0.1227 |
0.3528 |
0.3723 |
|
25.5 |
-0.0346 |
0.1227 |
0.3674 |
0.3813 |
|
27.5 |
-0.0494 |
0.1218 |
0.3821 |
0.3921 |
|
29.5 |
-0.0652 |
0.1218 |
0.3889 |
0.4011 |
|
31.5 |
-0.085 |
0.1199 |
0.4035 |
0.409 |
|
33.5 |
-0.1048 |
0.116 |
0.4133 |
0.4139 |
|
35.5 |
-0.1236 |
0.1189 |
0.4279 |
0.4198 |
|
37.5 |
-0.1463 |
0.1141 |
0.4347 |
0.4209 |
Nyomástényező
a felső felületen
|
X/H |
a=-2 |
a=0 |
a=6 |
a=10 |
|
-5 |
0.0178 |
0.0087 |
0.0039 |
-0.0108 |
|
3 |
0.0306 |
0.0414 |
0.0799 |
0.0896 |
|
5 |
0.03 |
0.0511 |
0.1248 |
0.1536 |
|
7 |
0.0296 |
0.0598 |
0.1627 |
0.1989 |
|
9 |
0.0425 |
0.081 |
0.1989 |
0.2471 |
|
11 |
0.0504 |
0.0993 |
0.232 |
0.2816 |
|
13 |
0.0454 |
0.1118 |
0.2612 |
0.3092 |
|
15 |
0.0336 |
0.1138 |
0.2846 |
0.3338 |
|
17 |
0.0286 |
0.1206 |
0.308 |
0.3545 |
|
19 |
0.0148 |
0.1216 |
0.3246 |
0.3683 |
|
21 |
0.001 |
0.1216 |
0.3402 |
0.3821 |
|
23 |
-0.0158 |
0.1207 |
0.3538 |
0.389 |
|
25 |
-0.0296 |
0.1236 |
0.3713 |
0.3979 |
|
27 |
-0.0474 |
0.1217 |
0.384 |
0.4029 |
|
29 |
-0.0642 |
0.1208 |
0.3947 |
0.4079 |
|
31 |
-0.0811 |
0.1189 |
0.4055 |
0.4178 |
|
33 |
-0.1038 |
0.116 |
0.4133 |
0.4178 |
|
35 |
-0.1236 |
0.1179 |
0.4298 |
0.4228 |
|
37 |
-0.1464 |
0.1131 |
0.4396 |
0.4239 |
5.
Részfeladat (3 pont)
Jelenítse
meg a sebesség szerint színezett áramvonalakat, a statikus-, az össznyomás eloszlást, valamint a turbulens kinetikai
energia eloszlását és mentse el az ábrákat TIF formátumban.
Röviden
fogalmazza meg a feladat célját, a megoldás módszerét és foglalja össze az
eredményeket.
Az önálló feladat eredményeit
PowerPoint (.PPT) formátumú dokumentumban készítse el,
majd töltse fel a személyes könyvtárába!