4. Csoportos
feladat: Henger körüli áramlás többféle
Reynolds-szám esetében
Alacsony Reynolds-szám tartományban (Re=50…200) egy tengelyére merőlegesen megfújt henger körül kétdimenziós időfüggő áramkép alakul ki. A homlokfalon képződő lamináris határréteg mindkét oldalon leválik, szabad nyírórétegeket képez, melyek a henger mögött nagy örvények formájában gyűlnek össze. A nagy örvények egymásra hatása következtében periodikus áramkép – az ismert Kármán-féle örvénysor – jön étre.
A feladat célja az áramkép megismerése több különböző Reynols-szám esetében és a számítások ellenőrzése mérési adatok alapján.
A számítási tartomány alakját és méreteit Bolló Betti (2010) tapasztalatai alapján az 1.ábrán látható módon írjuk elő. d¥/d arány értéke legyen 100. A tartomány határán mindenhol u¥ sebességet írjuk elő peremfeltételként.
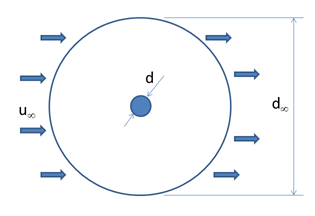
1.ábra Geometriai modell és peremfeltételek
1. Részfeladat (3
pont)
Geometriai modell és 6-8 ezer négyszög elemekből álló, struktúrált háló elkészítése.
2. Részfeladat (3
pont)
Áramló folyadékként levegőt válasszanak, a viszkozitás érétkét olyan módon vegyék fel, hogy a Reynolds-szám értéke a mérési adatok táblázatában megadott értékeknek feleljen meg! Végezzenek próbafuttatást, majd ellenőrizzék a Courant-szám megoszlását. Határozzák meg az időlépés nagyságát úgy, hogy a Courant-szám maximális értéke közelítőleg 1 legyen. Előzetesen feltételezve, hogy a periodikus áramkép eléréséhez 120 * d/u¥ idő szükséges, végezzenek becsülést a szükséges számítási időre! Szükség esetén módosítsák a hálót!
3 Részfeladat (3
pont)
Végezzenek szimulációt a periodikus áramkép eléréséig legalább 3 különböző Reynolds-számra, számítás közben figyelemmel kísérve a FL felhajtóerő és az FD ellenálláserő értékeit!
4. Részfeladat (3
pont)
Határozzák meg a periodikus áramkép esetében FD átlagértékét (FD,avg), továbbá FL frekvenciáját (f) és RMS értékét (FL,rms), majd ezek alapján határozzák meg az alábbi dimenzió nélküli mennyiségeket:
![]() ,
, ![]() ,
, ![]() .
.
Hasonlítsák össze számítási eredményeit az alábbi mérési adatokkal:
|
Re |
50 |
70 |
90 |
110 |
130 |
150 |
170 |
Referencia |
|
St |
0.122 |
0.144 |
0.159 |
0.169 |
0.177 |
0.183 |
0.189 |
Williamson
(1998) |
|
cL,rms |
0.0466 |
0.138 |
0.199 |
0.254 |
0.306 |
0.356 |
0.404 |
Norberg
(2001) |
|
cD,avg |
1.45 |
1.39 |
1.36 |
1.34 |
1.33 |
1.33 |
1.33 |
Henderson
(1995) |
1.táblázat Mérési adatok
5. Részfeladat (3
pont)
Röviden fogalmazzák meg a feladat célját és a megoldás módszerét, továbbá foglalják össze az eredményeket az áramkép, az időfüggvények és az átlagértékek bemutatásával!
A csoportos feladat eredményeit PowerPoint (.PPT) formátumú dokumentumban készítsék el, majd töltsék fel a személyes könyvtárakba!
Referenciák:
Bolló, B, Baranyi, L., 2010. Computation of low-Reynolds number flow around a stationary circular cylinder. Proc. 7th International Conference on Mechanical Engineering, Budapest, pp. 891-896.
Henderson, R.D., 1995. Details of the drag curve near the onset of vortex shedding. Physics of Fluids 7, 2102–2104.
Norberg, C., 2001. Flow around a circular cylinder: aspects of fluctuating lift. Journal of Fluids and Structures 15, 459-469.
Williamson, C.H.K., Brown, G.L., 1998. A series in 1/√Re to represent the Strouhal-Reynolds number relationship of the cylinder wake. Journal of Fluids and Structures 12(8), 1073-1085.